1611年,以行星运动定律而闻名的约翰内斯·开普勒(JohannesKepler)提出了一个解决方案,解决了有关如何以最密集的方式排列相等大小的球体的问题。当这位著名天文学家被问到如何堆叠炮弹以占用最少空间时,他回答了这个问题。开普勒得出的结论是,最好的配置是所谓的面心立方晶格,这是杂货店中常用的展示橙子的方法:每个炮弹都应该放在四个炮弹(紧密排列成两排)留下的空腔中。-两个正方形)位于其正下方。然而,这只是一个猜想,直到近400年后才被密歇根大学的一位数学家证明。
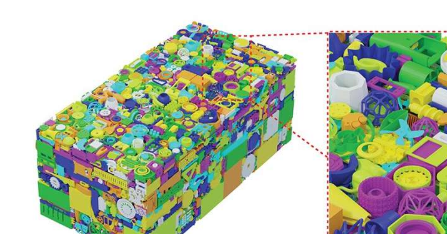
虽然这解决了均匀球体堆积的问题,但更普遍的问题(关于定位不同尺寸和形状的3D对象的最佳方式)仍未解决。事实上,这个问题被归类为NP难问题,这意味着如果不需要非常长的计算时间(可能需要数年或数十年,具体取决于问题的数量),就无法精确地(甚至近似地)解决该问题。需要装入有限空间的部件。
尽管如此,还是取得了一些重大进展,不是以数学证明的形式,而是通过一种新的计算方法,使这项以前难以处理的任务变得更加容易处理。由WojciechMatusik博士领导的来自MIT和Inkbit(一家位于马萨诸塞州梅德福的MIT衍生公司)的研究人员团队。'03,麻省理工学院教授兼Inkbit联合创始人,将于今年8月在SIGGRAPH2023(世界上最大的计算机图形和交互会议)上展示这项技术,他们称之为“密集、无互锁且可扩展的光谱封装”(SSP)技术。随附论文由Inkbit的QiaodongCui、麻省理工学院研究生VictorRongSM'23、DesaiChen博士撰写。'17(也是Inkbit),ACM图形交易。
SSP的第一步是制定用于填充固定容器的固体3D对象的顺序。例如,一种可能的方法是从最大的对象开始,以最小的对象结束。下一步是将每个对象放入容器中。为了促进这一过程,容器被“体素化”,这意味着它由由微小立方体或体素组成的3D网格表示,每个立方体或体素的大小可能只有一立方毫米。网格显示容器的哪些部分(或哪些体素)已被填充以及哪些部分是空的。
待包装的物体也被体素化,再次由与容器中尺寸相同的立方体聚集体表示。为了计算出该对象的可用空间,该算法随后计算每个体素处称为碰撞度量的量。它的工作原理是将对象的中心放置在容器中的每个体素处,然后计算对象重叠或“碰撞”的占用体素的数量。对象只能放置在重叠为零的位置,换句话说,没有碰撞的位置。
下一步是筛选所有可能的放置位置并确定放置对象的最佳可用位置。对于这项任务,研究人员在每个体素上计算另一个度量,该度量旨在局部最大化堆积密度。该指标测量对象与容器壁之间的间隙,或者正在移动的对象与已位于容器内的对象之间的间隙。例如,如果对象放置在正中心,则该指标可能会分配较高的值。
然而,目标是最小化对象之间的间隙,这可以通过将对象放置在度量值最低的位置来实现。“这有点像俄罗斯方块游戏,”马图斯克解释道。“你想留下尽可能少的空白空间。”
然而,这并不是故事的全部,因为前面的讨论涉及一个被移动或“平移”到容器中同时在空间中保持固定方向的物体。计算机可能会对同一对象使用许多不同的方向来经历整个过程,直到找到最适合空间的方向。
SSP算法的最后一步是确保,对于看似理想的排列,每个对象实际上都可以进入其指定的位置,或者等效地,当容器被拆包时,每个对象都可以与其他对象分离。也就是说,填料必须是“无互锁的”——这是避免诸如互锁环之类的配置的条件。
当容器填满时,找出每个对象的最佳放置位置显然需要大量计算。但该团队采用了一种数学技术,即快速傅立叶变换(FFT),该技术以前从未应用于打包问题。通过使用FFT,可以通过一组相对有限的计算(例如简单的乘法)来解决最小化体素重叠和最小化容器中所有体素间隙的问题,而不是测试对象的所有可能位置的不切实际的替代方案放置在里面。这使得打包速度提高了几个数量级。
在一次演示中,新算法在短短40秒内有效放置了670个物体,实现了约36%的堆积密度。耗时两个小时,排列好6596个物品,堆积密度为37.30%。“我们获得的密度接近40%,明显优于传统算法获得的密度,”Matusik说,“而且速度也更快。”
普渡大学计算机科学教授BedrichBenes评论说,这项工作代表了“有效组织3D对象这一长期存在问题的突破性解决方案”。“所提出的解决方案最大限度地提高了封装密度,并有可能在从机器人到制造的许多实际领域找到应用。此外,无联锁解决方案适用于计算机控制的环境。”
马图斯克表示,这种方法当然对仓库和运输公司很有用,因为这些公司通常将各种物品包装到不同尺寸的盒子中。然而,他和他的同事对3D打印(也称为增材制造)的应用特别感兴趣。零件通常批量生产并放置在托盘上。然而,Matusik表示,目前的方法“对[容器]体积的利用率非常有限”——通常约为20%。“如果我们能够提高封装密度,”他补充道,“我们就可以提高打印过程的整体效率,从而降低制造零件的总体成本。”
虽然SIGGRAPH论文为3D打印以及包装刚性物体提供了新的和改进的程序,但如何最好地排列可变形物体或铰接物体(后者由多个通过关节连接的刚性部件组成)的问题仍然悬而未决,并可能在未来的工作中得到解决。与此同时,如果人们发现自己只需两个小时即可将6,000多件物品放入储物箱中,也无需感到绝望。帮助可能只是一个算法而已。
